Løsningsforslag 1T eksamen V2023

Jeg blir veldig glad om du melder ifra om feil enten direkte til meg eller via forumet på matematikk.net.

Del 1

Oppgave 1

Alternativ 1

Vi har at $\sin u = \frac{8}{10}$ og $\cos u = \frac{6}{10}$ .

\sin^{2} u + \cos^{2} u = {(\frac{8}{10})}^{2} + {(\frac{6}{10})}^{2} = \frac{64}{100} + \frac{36}{100} = \frac{100}{100} = 1

Alternativ 2: bruke pytagoras

Vi har $\sin u = \frac{8}{10} ⟺ 8 = 10 \sin u$ og $\cos u = \frac{6}{10} ⟺ 6 = 10 \cos u$

Vi kan bruke pytagoras på trekanten og sette opp

\begin{aligned} 8^{2} + 6^{2} & = 10^{2} \\ {(10 \sin u)}^{2} + {(10 \cos u)}^{2} & = 10^{2} \\ 10^{2} \sin^{2} u + 10^{2} \cos^{2} u & = 10^{2} \\ \sin^{2} u + \cos^{2} u & = 1 \end{aligned}

$\underset{―}{\underset{―}{{(\sin u)}^{2} + {(\cos u)}^{2} = 1}}$ , som skulle vises.^[1]

Oppgave 2

Vi kan faktorisere ved hjelp av heltallsmetoden. Jeg ser at:

f (x) = x^{2} - 2 x - 8 = (x - 4) (x + 2)

Ved å sette funksjonen lik null finner jeg nullpunktene

\begin{aligned} f (x) & = 0 \\ (x - 4) (x + 2) & = 0 \\ x - 4 = 0 & \lor x + 2 = 0 \\ x = 4 & \lor x = - 2 \end{aligned}

Funksjonen krysser $x$ -aksen ved $x = 4$ og $x = - 2$ .

Oppgave 3

Hvis likningen skal være en identitet så må uttrykkene på høyre side og venstre side være like for alle $x$ .

Vi ser av faktoriseringen at $(x - 1)$ er en faktor i $x^{3} - 5 x^{2} - 8 x + 12$ . Det enkleste er nok derfor å dividere begge sider av likningen med $(x - 1)$ .^[2] Venstre side blir da:

\begin{aligned} (x^{3} - 5 x^{2} - 8 x + 12 & ) : (x - 1) = \underset{―}{x^{2} - 4 x + 12} \\ \underset{―}{x^{3} - 1 x^{2} + 0 x + 0} \\ - 4 x^{2} - 8 x + 12 \\ \underset{―}{- 4 x^{2} + 4 x + 0} \\ 12 x + 12 \\ \underset{―}{12 x + 12} \\ 0 \end{aligned}

Jeg utfører divisjonen på begge sider av den opprinnelige likningen og får

\begin{aligned} (x^{3} - 5 x^{2} - 8 x + 12) : (x - 1) & = (x - 1) (x + a) (x - b) : (x - 1) \\ \underset{heltallsmetoden gir (x + 2) (x - 6)}{\underset{⏟}{x^{2} - 4 x + 12}} & = (x + a) (x - b) \\ (x + 2) (x - 6) & = (x + a) (x - b) \end{aligned}

Jeg ser at $\underset{―}{\underset{―}{a = 2 \land b = 6}}$ for at likningen skal bli en identitet.

Oppgave 4

Jeg ser at vi skal lage en rasjonal funksjon på formen $f (x) = \frac{P (x)}{Q (x)}$ .

Det er en vertikal asymptote og bruddpunkt ved $x = 1$ , det betyr at uttrykket i nevneren vår må ha nullpunkt i $x = 1 ⟹ Q (1) = 0$ .

Det er en horisontal asymptote ved $y = 3$ . Det betyr at $lim_{x \to \pm \infty} \frac{P (x)}{Q (x)} = 3$ . For at det skal være mulig må polynomene i teller og nevner ha samme grad. Dette ligner på en rasjonal funksjon med førstegradsuttrykk i teller og nevner der koeffisienten foran $x$ i telleren er 3 ganger så stor som koeffisienten foran $x$ i nevneren.

Jeg lar $Q (x) = x - 1$ siden dette er et førstegradsuttrykk som vil gi riktig bruddpunkt.

Vi har nå tre krav til $P (x)$ :

$P (x)$ skal ha samme grad som $Q ⟹ P$ må være førstegradsuttrykk $a x + b$
$P (x)$ skal ha 3 ganger så stor koeffisient som $Q (x) ⟹ P (x) = 3 x + b$
$f (x)$ har et nullpunkt i $x = 2 ⟹ P$ skal ha nullpunkt i $x = 2 ⟹ P (2) = 0$

For å oppfylle det siste kravet må $P$ være på formen $P (x) = 3 x + b$ , der $b$ må være slik at $P (2) = 0$ .

\begin{aligned} P (2) & = 0 \\ 3 \cdot 2 + b & = 0 \\ b & = - 6 \end{aligned}

Et funksjonsuttrykk som passer til grafen er

\underset{―}{\underset{―}{f (x) = \frac{3 x - 6}{x - 1}, D_{f} = R ∖ 1}}

Kommentar: Jeg tolker oppgaveteksten som at vi skal finne én funksjon $f (x)$ som passer til grafen. Generelt vil alle uttrykk på formen $\frac{3 c x - 6 c}{c x - c}$ der $(c \in R) \land (x \in R ∖ 1)$ passe til grafen, så det kan godt være at dette generelle uttrykket er et bedre svar på oppgaven.

Oppgave 5

Jeg vet at den deriverte er null i de stasjonære punktene til en funksjon. Når den deriverte er positiv så vokser grafen. Når den deriverte er negativ så minker grafen.

Jeg ser at $f$ har bunnpunkt i $x = - 3, 12$ og $x = 5, 12$ (det må være bunnpunkt siden den deriverte beveger seg fra den negative siden til den positive siden ved disse punktene). $f$ må, med samme begrunnelse, ha et toppunkt i $x = 1$ .

Vi har nullpunkter ved $x = - 4$ , $x = - 2$ , $x = 4$ og $x = 6$ .^[3]

For å skissere grafen så starter jeg med nullpunktene og tegner inn passende bunnpunkter og toppunkt ved $x$ -verdiene jeg fant tidligere.

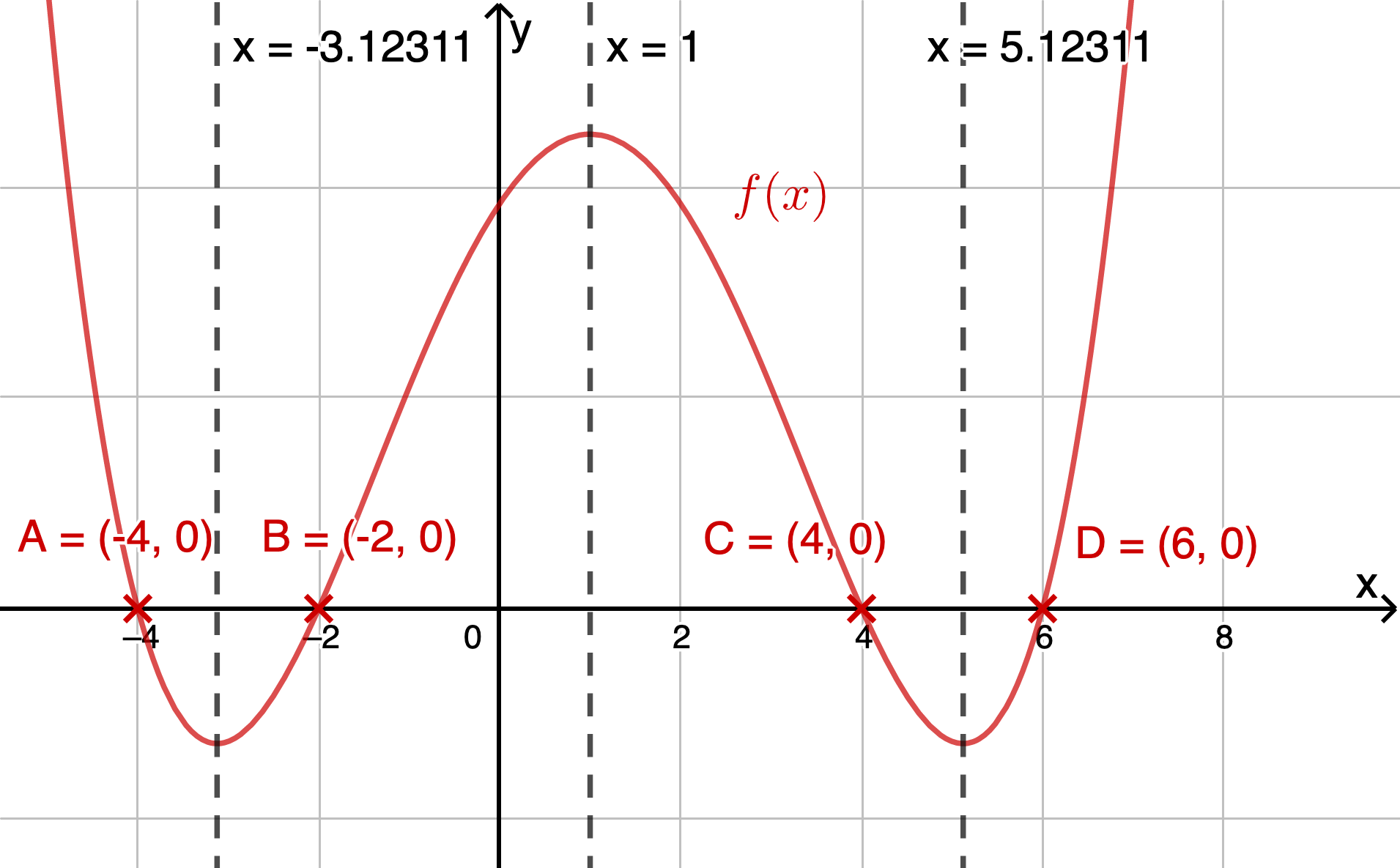
Del 1 oppgave 5. Skisse av fjerdegradsfunksjon

\clearpage

Del 2

Oppgave 1

1a

Jeg tegnet grafen til funksjonen og fant skjæringspunktene ved $x$ -aksen, hvor temperaturen er 0 °C, se punkt $B$ og $C$ .

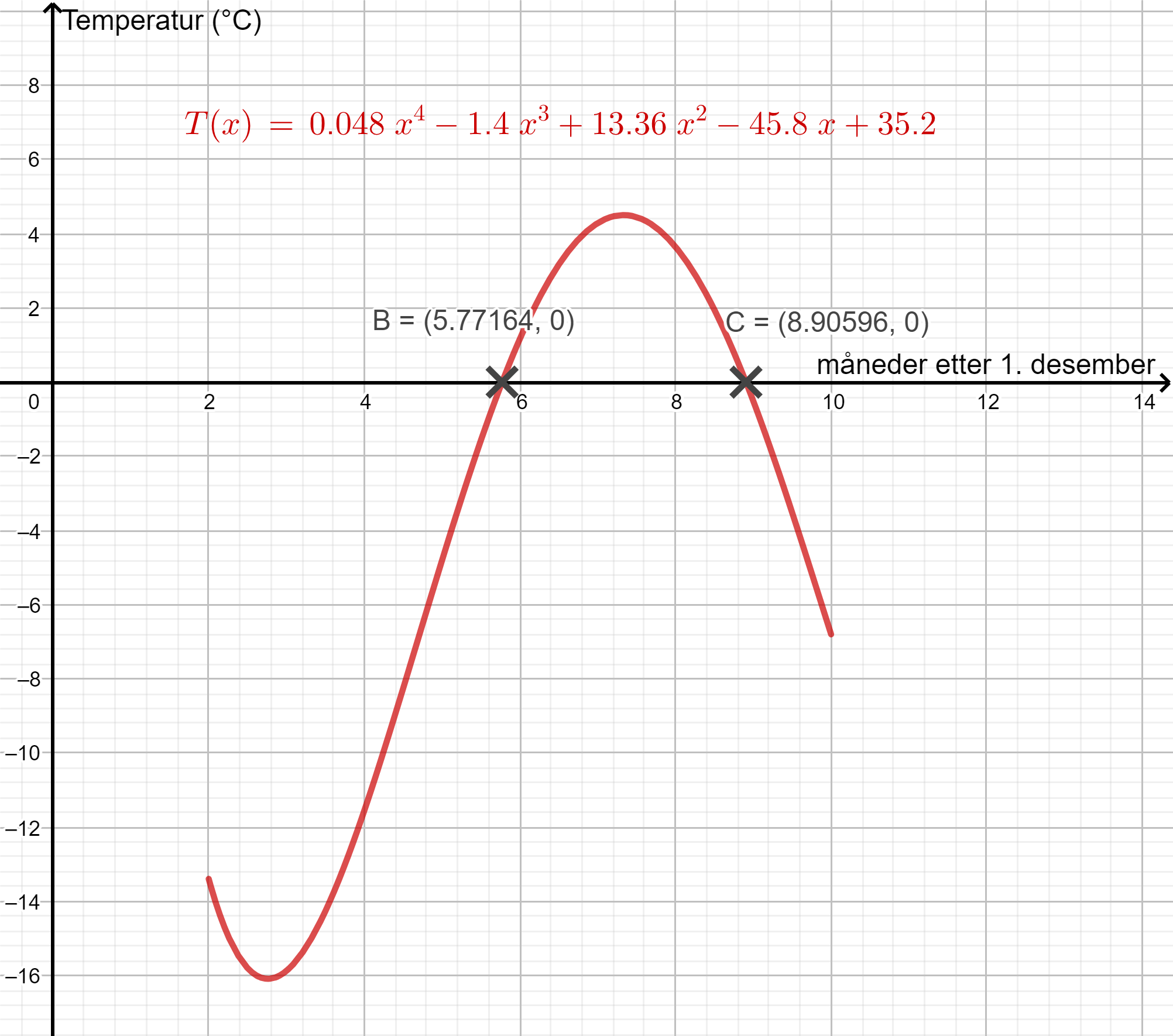
Del 2 oppgave 1. Gjennomsnittemperatur på Svalbard 1. februar–1. oktober

Det er $8, 906 - 5, 772 = 3, 134$ måneder mellom skjæringspunktene. Jeg setter at det er 30,5 døgn i hver måned slik at vi får:

3, 134 \cdot 30, 5 = 95, 6 \approx \underset{―}{\underset{―}{96}}

Temperaturen er over 0 °C i omtrent 96 døgn

1b

Jeg la inn punktene i GeoGebra, dro en linje mellom dem og fant stigningstallet, se $b = 5.04$ i utklippet.

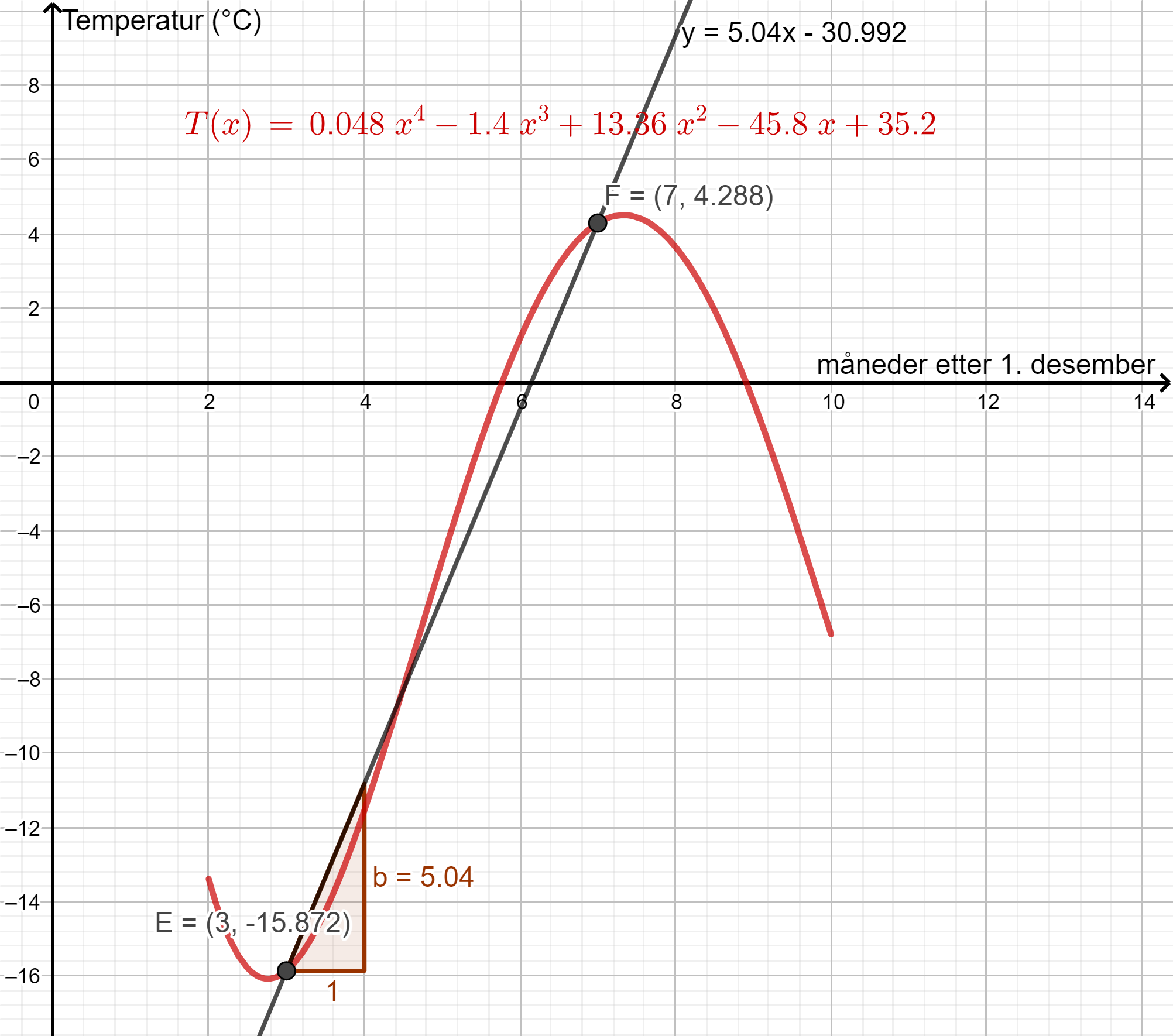
Del 2 oppgave 1b. Gjennomsnittlig vekstfart fra mars til juli

Stigningstallet til linja gir den gjennomsnittlige vekstfarten fra $x = 3$ til $x = 7$ .

Temperaturen steg med 5,04 grader per måned i gjennomsnitt i perioden fra 1. mars til 1. juli.

1c

Jeg tegnet $T^{'}$ sammen med $T$ i koordinatsystemet og fant nullpunkter og ekstremalpunkter til $T^{'}$ .

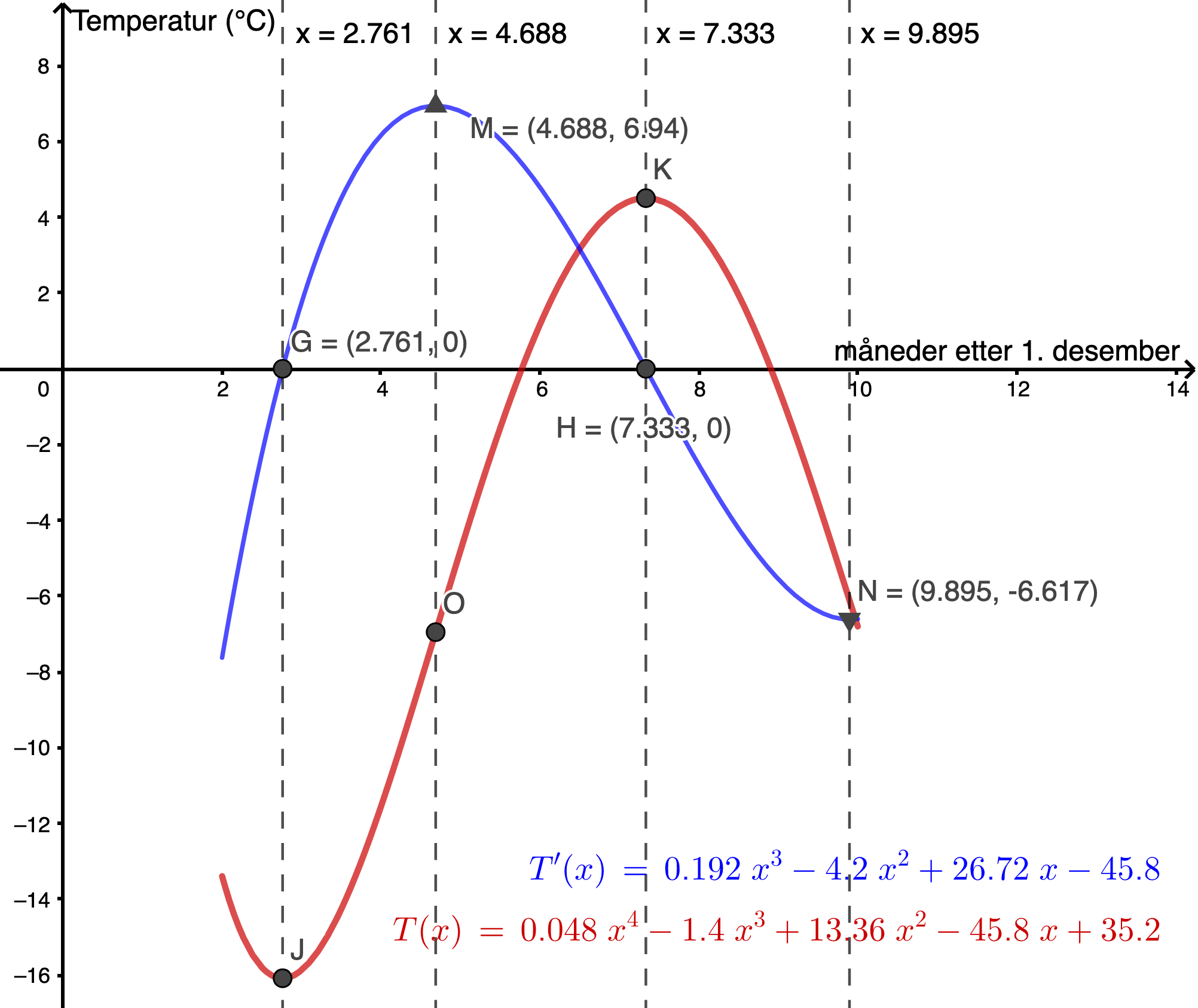
Del 2 oppgave 1c. Vekstfarten til temperaturen på Svalbard

\begin{aligned} Toppunkt (M) : & (4, 69, 6, 94) \\ Bunnpunkt (N) : & (9, 90, - 6, 62) \\ Nullpunkter (G og H): & (2, 76, 0) og (7, 33, 0) \end{aligned}

Jeg sammenlignet disse punktene med tilsvarende punkter på grafen til $T$ .

Nullpunktene til $T^{'}$ ligger ved samme $x$ -verdi som ekstremalpunktene til $T$ . $y$ -koordinatene til nullpunktene til $T^{'}$ er selvsagt null, og det stemmer godt med at vekstfarten i ekstremalpunktene til $T$ er null. Ved hjelp av nullpunktene til $T^{'}$ finner vi den kaldeste temperaturen i bunnpunktet 23. februar og den varmeste temperaturen i toppunktet 10. juli.

Toppunktet til $T^{'}$ er er ved $x = 4, 69$ og $y = 6, 94$ . Det vil si at rundt den 21. april vil temperaturen øke raskest. Gjennomsnittstemperaturen stiger raskest med 6,94 grader per måned rundt 21. april.

Bunnpunktet til $T^{'}$ er er ved $x = 9, 90$ og $y = - 6, 62$ . Det vil si at rundt den 27. september vil temperaturen synke raskest. Gjennomsnittstemperaturen synker raskest med 6,62 grader per måned rundt 27. september.

Oppgave 2

2a

Med 80 m tau og et område med lengde 60 m så har de 20 m igjen å fordele til de to siste sidene. Matematisk kan vi skrive $\frac{80 - 60}{2} = 10$ . Bredden blir altså 10 m.

A = 10 \cdot 60 = 600

Arealet av området er 600 m².

2b

Jeg satte opp en oversikt i Excel, se formlene i formelutklippet. Vi ser at arealet øker når bredden øker helt fram til lengden er 40 m og bredden er 20 m, deretter minker arealet.

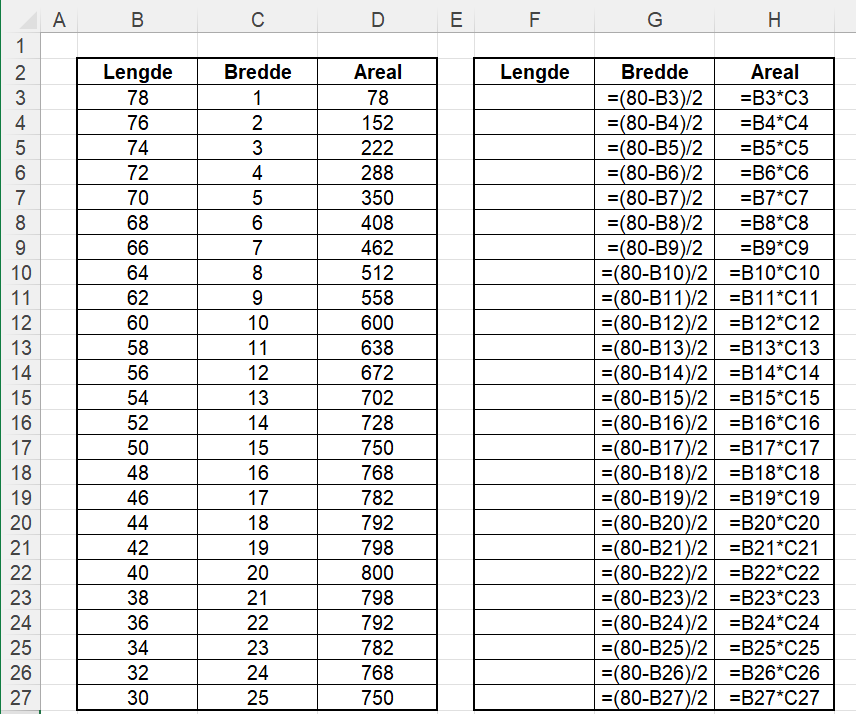
Del 2 oppgave 2b. Oversikt over lengde og bredde av teltplass

Hermann har rett i at vi får det største arealet dersom lengden er dobbelt så lang som bredden.

2c

La oss kalle bredden i meter for $x$ . Da må lengden i meter være $80 - 2 x$ . Vi kan sette opp et funksjonsuttrykk for arealet $A (x)$ der bredden er $x$ meter.

A (x) = (80 - 2 x) \cdot x

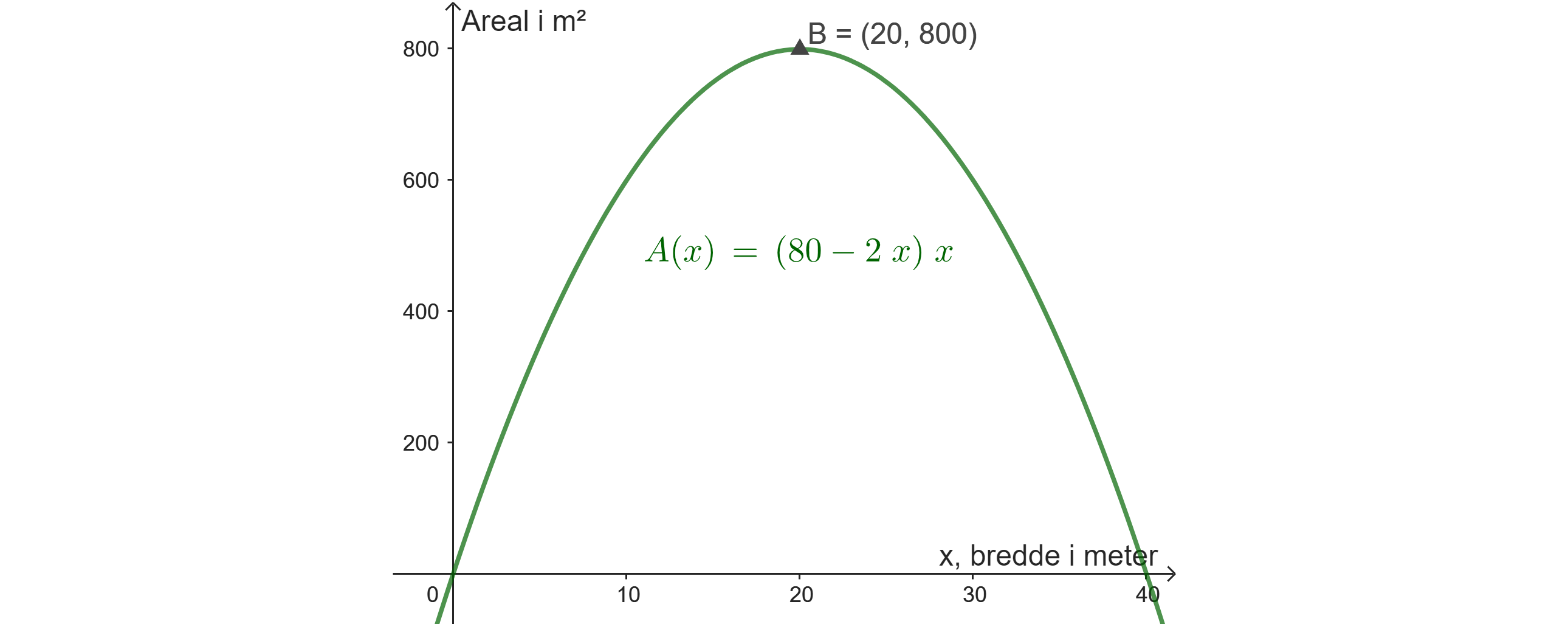Del 2 oppgave 2c. Areal av teltplass som funksjon av bredden \

Jeg tegnet denne grafen i GeoGebra og fant toppunktet, se punkt $B$ .
Toppunktet ligger ved bredden $x = 20$ , så Hermann sin påstand er riktig.

Oppgave 3

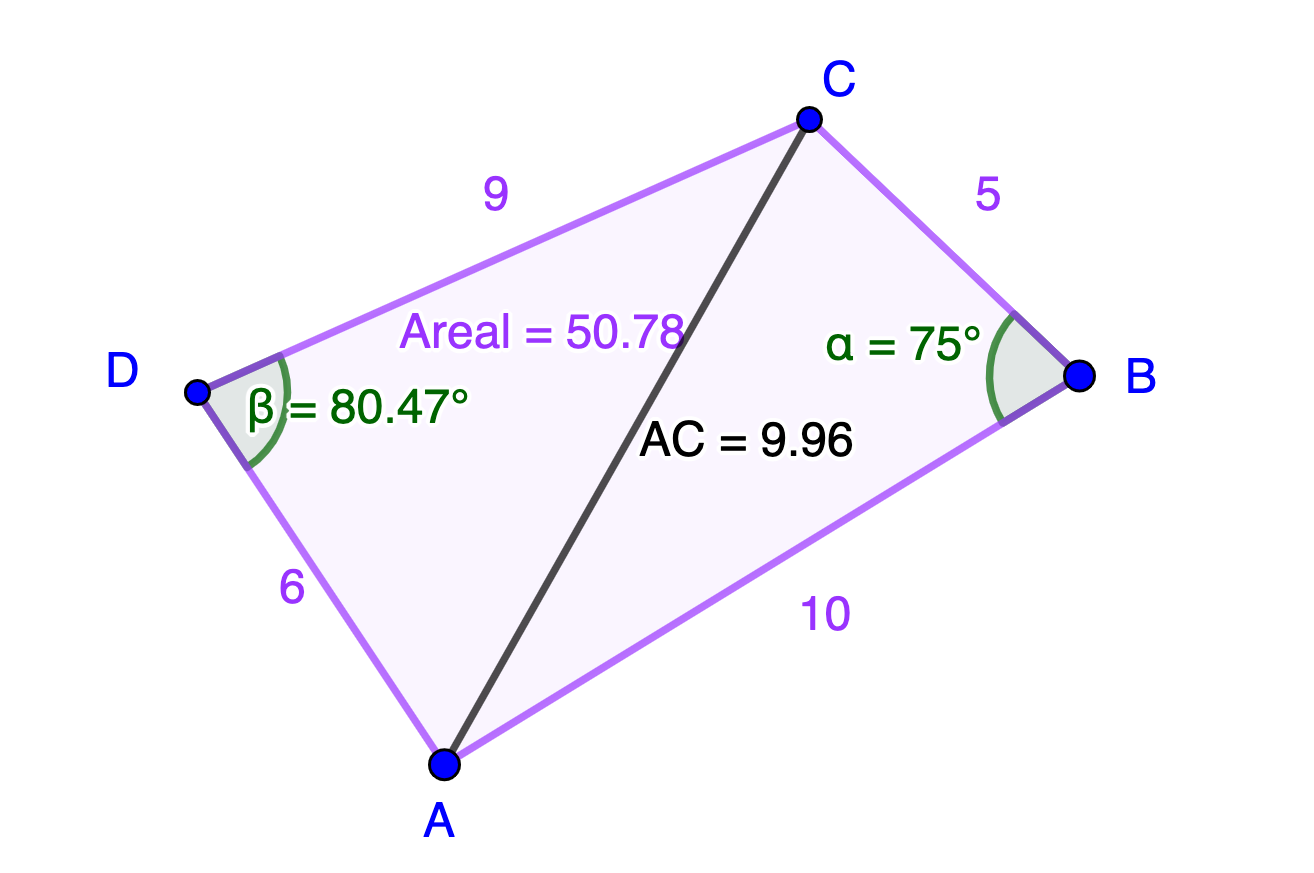
Del 2 oppgave 3. Skisse av

Jeg delte firkant $A B C D$ i to trekanter: $A B C$ og $A C D$ , se den vedlagte skissen. Jeg brukte cosinussetningen på $A B C$ med $A C$ som den ukjente siden, se linje 5 i CAS. På den måten fant jeg $A C^{2} = 99, 12$ .

$A C^{2}$ kunne jeg bruke til cosinussetningen på trekant $A C D$ . Jeg kjente nå alle de tre sidene slik at kunne jeg bestemme $∠ D = 80, 47 °$ i linje 6.

For å finne arealet av $◻ A B C D$ brukte jeg arealsetningen på begge trekantene og la sammen de to arealene i linje 7.

Arealet av $◻ A B C D$ er 50,78.

Oppgave 4

4a

Jeg ser at alle rektanglene har bredde 1. Arealet av hvert rektangel er derfor $A_{◻} = h \cdot b = h \cdot 1 = h$ . Høyden til rektangelet er gitt ved $f (x) = \frac{1}{9} (x + 1) (x - 6)^{2}$ hvor $x \in {0, 1, 2, 3, 4, 5}$ .

Jeg legger sammen funksjonsverdiene i CAS og finner at det samlede arealet er

A = \underset{―}{\underset{―}{\frac{196}{9}}}

4b

def f(x):
    return 1 / 9 * (x + 1) * (x - 6) ** 2   # Definerer funksjonen


x_min = 0                                   # Startverdi for x
x_maks = 6                                  # Sluttverdi for x

n = 6000                                    # antall rektangler

bredde = (x_maks - x_min) / n               # bredden av hvert rektangel

x = x_min                                   # vi starter med å finne
                                            # f(x) ved f(x_min)
areal = 0                                   # lager en variabel som summerer
                                            # arealet
for i in range(n):
    areal_rektangel = bredde * f(x)         # beregener arealet til rektangelet
    areal = areal + areal_rektangel         # summerer arealet av rektangelet
                                            # og det totale arealet
    x = x + bredde                          # flytter x-verdien bortover langs
                                            # x-aksen tilsvarende bredde av rekt
print(f"Arealet av rektanglene er {areal:.3f}")

4c

Bruker programmet jeg lagde i 4b. Det gir utskriften Arealet av rektanglene er 20.002.

Oppgave 5

Jeg ser at $△ S B C$ og $△ A B S$ er likebeinte trekanter med to sider med lengde $r$ .

Jeg har fått oppgitt arealet $A = 2 \sqrt{3} + 6$ , derfor ønsker jeg å bruke arealsetningen til å bestemme $r$ . Jeg ser at det er mulig å bruke arealsetningen med $B C$ , $A B$ og $∠ B$ .

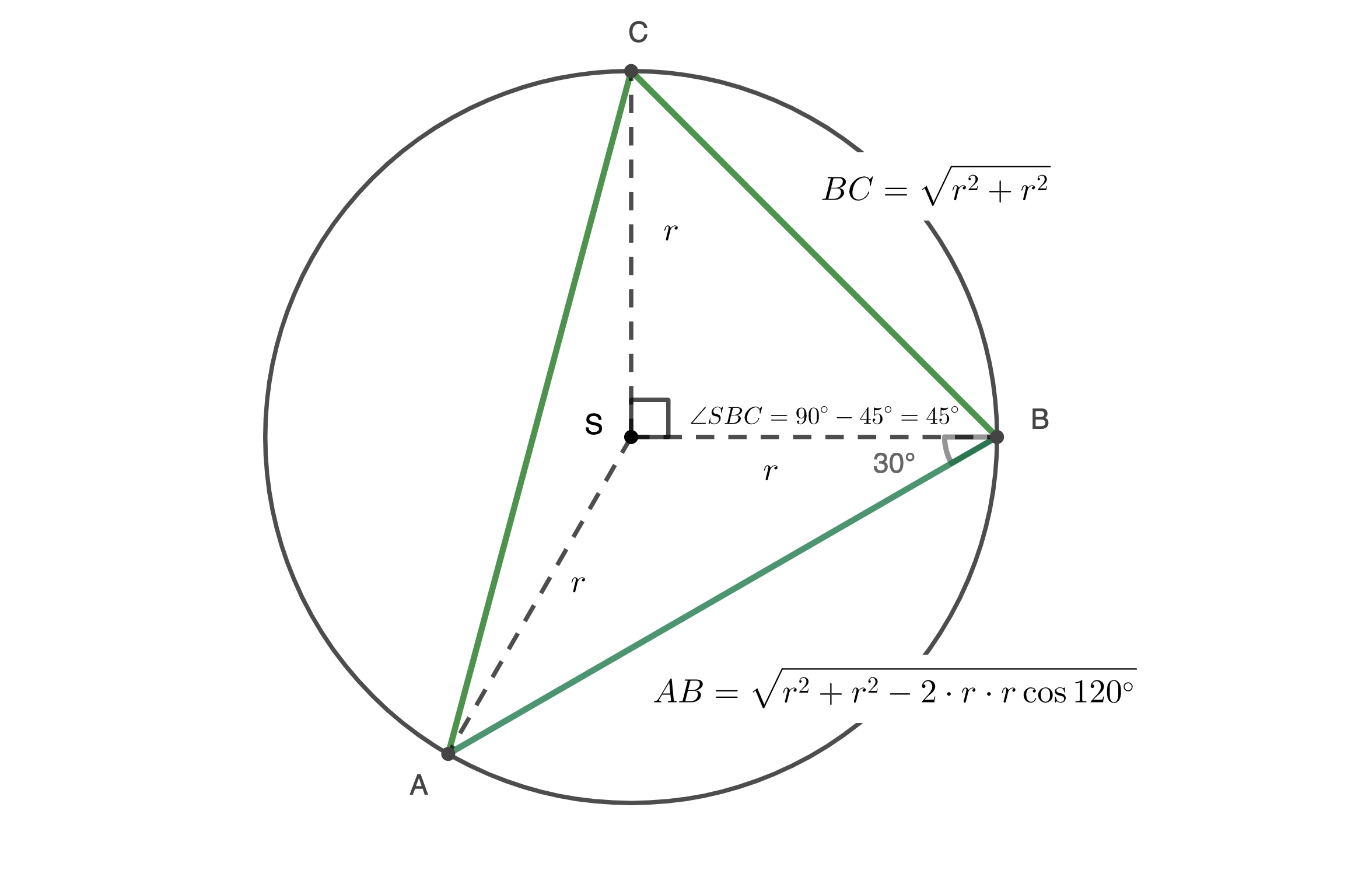
Del 2 oppgave 5. Skisse av figuren

For å bestemme $B C$ brukte jeg pytagoras i linje 1 og fant $B C = \sqrt{2} | r |$ . Dette er lik $\sqrt{2} r$ siden radius alltid må være positiv.

For å bestemme $A B$ fant jeg først vinkelen $∠ S A B = ∠ S B A = 30 °$ siden $△ A B S$ er likebeint. Da må $∠ A S B = 120 °$ . Deretter brukte jeg cosinussetningen i linje 2 på trekant $A B S$ med $A B$ som den ukjente siden. Igjen kan vi se bort fra negative løsninger og $A B = \sqrt{3} r$ .

Siden $△ S B C$ er rettvinklet og likebeint må $∠ S B C = 45 °$ . Jeg satt derfor opp arealsetningen på $△ A B C$ i linje 3 og løste likningen med det oppgitte arealet i linje 4.

\underset{―}{\underset{―}{r = 2 \sqrt{2}}}

Oppgave 6

6a

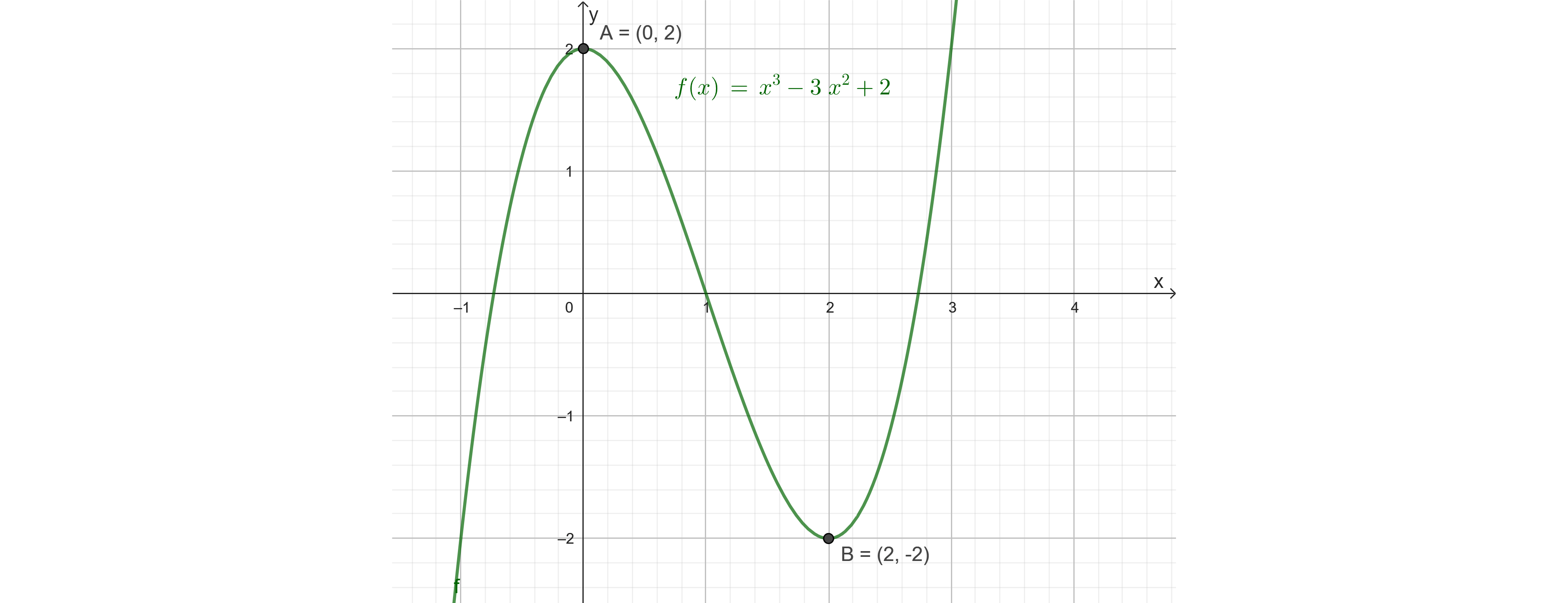
Jeg tegnet grafen til $f$ i GeoGebra og fant ekstremalpunktene, se $A$ og $B$ i utklippet.

$f$ har toppunkt i $(0, 2)$ og bunnpunkt i $(2, - 2)$ .

6b

Tredjegradsfunksjoner uten førstegradsledd har den generelle formen

P (x) = a x^{3} + b x^{2} + c

Den deriverte $P^{'} (x)$ gir oss den momentane vekstfarten for hver $x$ -verdi. Når den momentane vekstfarten er lik null så verken vokser eller minker funksjonen $⟹$ vi må da befinne oss i et stasjonært punkt.

\begin{aligned} P^{'} (x) & = 3 a x^{2} + 2 b x \\ 0 & = 3 a x^{2} + 2 b x \\ 0 & = (3 a x + 2 b) x \\ 3 a x + 2 b = 0 & \lor x = 0 \\ 3 a x = - 2 b & \lor x = 0 \\ x = \frac{- 2 b}{3 a} & \lor x = 0 \end{aligned}

Vi ser at $x = 0$ alltid vil gi et stasjonært punkt i $(0, P (0))$ for slike tredjegradsfunksjoner. Stasjonære punkter er ikke bare topp- eller bunnpunkter, det kan også være terrassepunkter slik som grafen til $x^{3}$ viser.

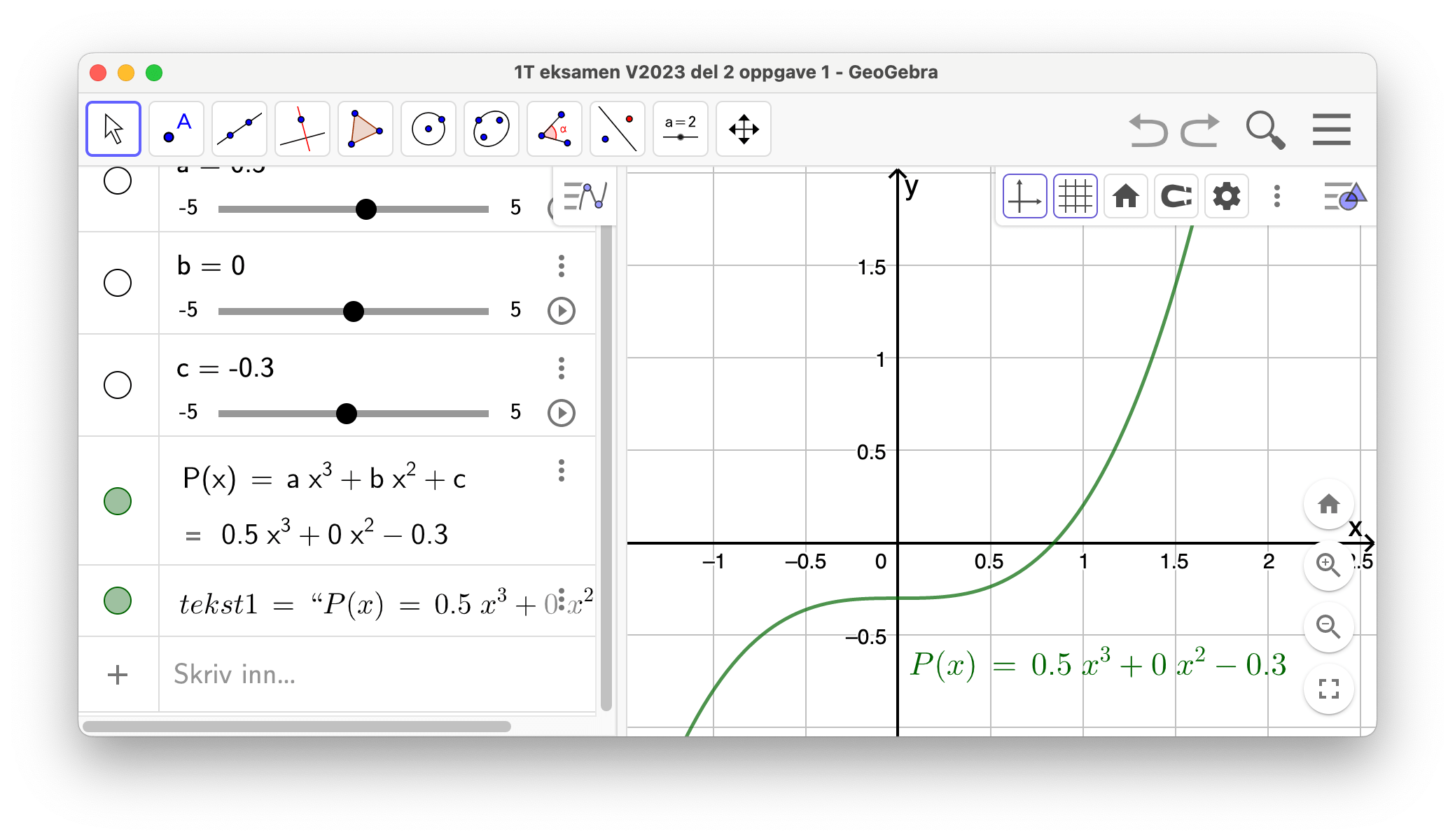
Del 2 oppgave 6b. Bruk av glidere til utforskning

Ved å tegne grafen til $P (x) = a x^{3} + b x^{2} + c$ i GeoGebra og justere på glidere for $a, b, c$ så ser det ut til at vi kun får terrassepunkter dersom $b = 0$ . Hvis $b \neq 0$ så ser det ut til at vi får både et toppunkt og et bunnpunkt. Hvis $b > 0$ så er det bunnpunktet som befinner seg på $y$ -aksen og hvis $b < 0$ så er det toppunktet som befinner seg på $y$ -aksen. Det ser også ut til at topp- og bunnpunktet går nærmere hverandre når jeg justerer $b$ slik at den blir nærmere 0.

Vi kan også se at $b = 0$ vil gi et terrassepunkt fra løsningene av $P^{'} (x) = 0$ som vi fant tidligere. Den ene løsningen vil alltid være $x = 0$ . Den andre løsningen, $x = \frac{- 2 b}{3 a}$ , vil også bli null dersom koeffisienten foran andregradsleddet, $b$ , er lik null. Dermed vil på vår toppunktsløsning og bunnpunktsløsning ligge i det samme punktet $⟹$ vi får et terrassepunkt.

Trym sin regel er nesten riktig. Det vil alltid være et topp- eller bunnpunkt på $y$ -aksen dersom tredjegradsfunksjonen mangler førstegradsledd, men har et andregradsledd. Det vil imidlertid alltid være et stasjonært punkt på $y$ -aksen dersom funksjonen mangler førstegradsleddet.

\clearpage

Alternative løsninger

Del 2 oppgave 4b

Denne løsningen er omtrent 3 ganger så kjapp og bruker lister istedenfor en løkke (men den krever også numpy biblioteket).

import numpy as np
def f(x):
    return 1 / 9 * (x + 1) * (x - 6) ** 2   # Definerer funksjonen


x_min = 0                                   # Startverdi for x
x_maks = 6                                  # Sluttverdi for x

n = 6000                                    # antall rektangler

bredde = (x_maks - x_min) / n               # bredden av hvert rektangel

x = np.linspace(x_min, x_maks, n+1)         # lager array med x-verdier
y = f(x)                                    # regner ut funksjonsverdien
                                            # f(x) for hver x
areal = sum(f(x)*bredde)                    # multipliserer bredde med høyde
											# og summerer til slutt
print(f"Arealet av rektanglene er {areal:.3f}")

Om løsningsforslaget

Løsningsforslaget er skrevet på privat initiativ. Det kan være flere feil i løsningene, det kan være ufullstendige løsninger og det kan finnes mange ulike strategier for løsning av de ulike oppgavene. Jeg setter veldig stor pris på tilbakemeldinger (spesielt om feil). Meld fra på forumet på matematikk.net eller direkte til meg.

Du står helt fritt til å bruke tekst, formler og bilder fra dette løsningsforslaget. En visning av kildedokumentet som er blitt brukt for å produsere PDF-versjonen finner du på https://raw.githubusercontent.com/stalegjelsten/stales-notater/main/src/site/notes/Publisert/Løsningsforslag 1T eksamen V2023.md

$\sin^{2} u$ er annen notasjon for ${(\sin u)}^{2}$ . Uttrykkene betyr nøyaktig det samme. ↩︎
Det er også mulig å gange ut parentesene på høyre side og sammenligne like ledd for å finne $a$ og $b$ , men det krever nok mer arbeid. ↩︎
Nullpunktene til $f$ gir oss mulighet til å lage et funksjonsuttrykk for en fjerdegradsfunksjon: $f (x) = a (x + 4) (x + 2) (x - 4) (x - 6)$ , men det er ikke meningen at du skal bruke funksjonsuttrykket og regne ut verditabell. ↩︎